Математики Андраш Мате и Олег Пихурко из Уорикского университета, Великобритания, и Джонатан Ноэль из Университета Виктории, Канада, нашли решение одной из неразрешимых математических задач античности о квадратуре круга, которую при помощи циркуля и линейки не решить, пишет американское издание по естественным и точным наукам Quanta Magazine.

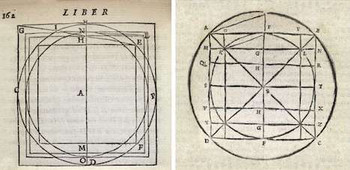
Одна из древнейших задач греческих математиков состояла в построении при помощи линейки и циркуля квадрата, равновеликого по площади к заданной окружности.

Коллектив из математиков Канады и Великобритании продемонстрировал, что круг можно трансформировать в квадрат, разрезав его на многочисленные части. При этом процесс можно визуализировать.

В статье Quanta Magazine ссылаются на вывод немецкого математика Фердинанда фон Линдеманна (1852-1939), который в 1882 году доказал, что решение квадратуры круга невозможно при помощи классических инструментов планиметрии. Линдеман был наиболее известен доказательством трансцендентности числа π (Пи).

В 1924 году польско-американский математик Альфред Тарский (1901-1983) изменил правила задачи. В соответствии с парадоксом теории множеств: он предложил разрезать круг на конечное число частей и собрать из них квадрат такой же площади. В исходном варианте речь шла о шаре в евклидовом пространстве, из которого можно путём операций разрезания и склейки получить два шара, по объему равных исходному. То есть речь шла о разбиении круга на конечное число подмножеств, которые попарно не пересекаются, и передвинуть их так, чтобы получить разбиение квадрата такой же площади на попарно непересекающиеся подмножества.

В 1990 году венгерский математик Миклош Лацкович (род. в 1948 году) решил задачи Тарского о квадратуре круга. Он подсчитал, что круг придется разрезать на более чем на 1050 частей. Однако математики сочли доказательство Лацковича "неконструктивным", поскольку он не визуализировал его.

Мате, Пихурко и Ноэль смогли визуализировать решение квадратуры круга. Несмотря на большое число фрагментов, весь ход преобразования теперь можно пошагово изобразить от начала до конца.